Algoritmo para factorizar N
December 23, 2024 16:51
En este artículo, vamos a explorar un algoritmo para factorizar un número N.
La factorización de un número es un proceso fundamental en matemáticas y ciencias de la computación, ya que nos permite descomponer un número en sus factores primos o divisores. Aunque puede parecer una tarea sencilla, existen varios enfoques y optimizaciones que pueden hacerla más eficiente, especialmente cuando el número N es grande.
Para diseñar este algoritmo, comenzamos por identificar que, en lugar de verificar todos los números hasta N, podemos reducir la búsqueda de divisores hasta la raíz cuadrada de N. Esto se debe a que si N tiene un divisor mayor que su raíz cuadrada, el otro divisor será menor, por lo que no es necesario seguir buscando más allá de ese punto.
A partir de allí, implementamos un ciclo que va desde 2 hasta la raíz cuadrada de N, dividiendo N por cada número en ese rango. Si encontramos que la división es exacta, guardamos el divisor y seguimos buscando.
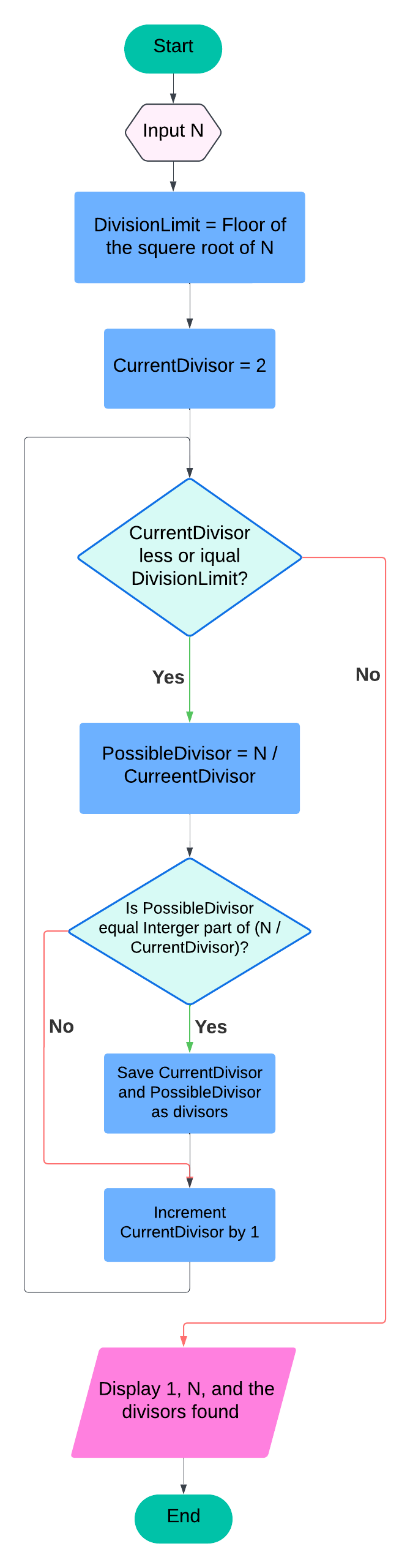
Este algoritmo no solo es eficiente, sino que también es fácil de implementar. A lo largo del artículo, proporcionamos un diagrama de flujo y un pseudocódigo que ilustran claramente cada paso del proceso.
¡Vamos a profundizar en cómo podemos poner este algoritmo en práctica!
Definición de factorización (Entender el problema)
La factorización de un número es el proceso de descomponerlo en un conjunto de factores que, multiplicados entre sí, dan como resultado el número original. Estos factores pueden ser cualquier tipo de números enteros, no necesariamente primos, y pueden ser números compuestos o incluso el mismo número 1.
Cuando hablamos de factorización en un sentido amplio, podemos referirnos a todas las maneras en que un número puede expresarse como un producto de factores enteros. Pero no todas esas expresiones se consideran "factorizaciones completas" o "factorizaciones fundamentales", ya que algunas de ellas no son tan informativas desde una perspectiva matemática.
En un sentido más general, cualquier número entero positivo puede ser factorizado en productos de factores enteros. Para 12, los factores enteros de 12 serían: 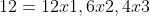
Sin embargo, normalmente se habla de factorización completa o factorización no trivial cuando estamos buscando factores que no sean simplemente el número mismo (12) ni el 1. Si sólo tomamos las factorizaciones no triviales, entonces las posibles factorizaciones de 12 son:
Este es el caso más específico, donde buscamos descomponer un número en factores primos. La factorización prima de 12 es:
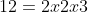
¿Cómo encontrar todos los divisores de un número N en la factorización de números enteros y completa?
-
Calcular la raíz cuadrada de N:
- Calculamos la raíz cuadrada de
N, solo necesitamos probar divisores hasta el valor entero de la raíz cuadrada. - Por ejemplo, para
N=45, la raíz cuadrada de45es aproximadamente6.7082. Por lo tanto, solo necesitamos probar los números desde2hasta6(la raíz cuadrada entera de45).
- Calculamos la raíz cuadrada de
-
Probar divisores:
-
Ejemplo con
45:- La raíz cuadrada de
45es aproximadamente6.7082, así que solo necesitamos probar los divisores hasta6. - Dividimos
45entre los números2,3,4,5,6:45 ÷ 2 = 22.5(no es un divisor exacto).45 ÷ 3 = 15(es un divisor exacto).45 ÷ 4 = 11.25(no es un divisor exacto).45 ÷ 5 = 9(es un divisor exacto).45 ÷ 6 = 7.5(no es un divisor exacto).
- Los divisores que encontramos son
3,15,5y9. - También incluimos en la respuesta al
1y a45
- La raíz cuadrada de
Start
obtain N
calculate DivisionLimit = Floor(SquareRoot(N))
set CurrentDivisor = 2
repeat-until CurrentDivisor > DivisionLimit
if CurrentDivisor <= DivisionLimit then
calculate PossibleDivisor = N / CurrentDivisor
if PossibleDivisor == IntegerPart(N / CurrentDivisor) then
save CurrentDivisor and PossibleDivisor as divisors
else
calculate CurrentDivisor = CurrentDivisor + 1
end-if
else
calculate CurrentDivisor = CurrentDivisor + 1
end-if
repeat-until wrong
display 1, N, and the divisors found
End
El algoritmo implica los siguientes pasos principales:
-
Calcular la raíz cuadrada de N:
- Esto se puede hacer en tiempo O
(log N), porque la mayoría de los métodos modernos para calcular raíces cuadradas utilizan iteraciones logarítmicas (e.g., método de Newton).
- Esto se puede hacer en tiempo O
-
Probar divisores desde 1 hasta la raíz cuadrada entera de N
-
Registrar los pares de divisores:
-
Por cada divisor
dencontrado, el cocienteN/dse calcula y se guarda. Esto también es una operación O(1)por divisor. -
Como máximo, encontramos la raíz cuadrada entera de
Nde divisores (en pares), por lo que este paso también tiene un costo de.
En total, la complejidad temporal del algoritmo es:
porque el cálculo de divisores domina el tiempo de ejecución.
-
El algoritmo requiere almacenar los divisores encontrados y sus correspondientes pares. Analicemos esto:
-
Espacio para los divisores:
-
Variables auxiliares:
- El algoritmo utiliza variables para
N,d(el divisor actual), la lista de divisores, y posiblemente otras variables para los resultados. Todas estas requieren espacio constante adicional (O(1)).
Por lo tanto, la complejidad espacial total del algoritmo es: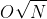
-
Raíz cuadrada de N
- La raíz cuadrada entera de ⌊4530940⌋=2129 (redondeamos hacia abajo).
-
Iteración hasta 2129
- El algoritmo prueba cada número entero
ddesde1hasta2129 - Para cada
d- Se verifica si
Nmod d=0 (Operación de residuo) - Si
des un divisor, se calcula su par complementarioN/d-
- Se verifica si
- En el peor caso, se realizan
2129divisiones y verificaciones del residuo.
- El algoritmo prueba cada número entero
-
Divisores complementarios:
- Para cada divisor
dencontrado, el divisor complementarioN/dtambién se registra si es diferente ded.
Por ejemplo, si
d=1, el complemento es 4530940, y sid=2, el complemento es 2265470. - Para cada divisor
-
Número total de operaciones:
-
En cada iteración, realizamos una división y verificamos divisibilidad. Esto resulta en
operaciones.
-
Cada divisor tiene un complemento, así que el número total de divisores registrados puede llegar a
2 x cantidad de divisores únicospara N = 4530940, estos divisores naturales son:en total 18 divisores, considerando complementos.
-
-
Número final de operaciones
Análisis espacial (Uso de la memoria)
Almacenamiento de divisores naturales:
- Como buscamos todos los divisores, debemos guardar cada divisor d y su complemento N/d.
- Si hay
Ddivisores únicos, el almacenamiento será2D.
En este caso, D=9, por lo que:
2D×4 bytes (por entero) =18 × 4 = 72 bytes
Variables auxiliares:
N,d, raíz cuadrada(N):3 x 4bytes= 12bytes.
Memoria total requerida:
- Divisores: 72 bytes-
- Variables auxiliares: 12 bytes-
- Total: 84 bytes.
En este artículo hemos explorado un proceso simple para encontrar los divisores de un número entero N, de forma eficiente, A través del análisis previo (revisando los conceptos matemáticos al rededor de este tema), detallamos cómo utilizar la raíz cuadrada de N para establecer un límite en el cual buscar divisores. Luego, podemos ver todo el proceso de cómo dividir N por un número i (empezando desde 2) y verificar si la división produce un número entero, lo que indica que i es un divisor de N.
A lo largo de esta explicación, proporcionamos un diagrama de flujo para visualizar el proceso paso a paso, mejorando la comprensión del algoritmo. También ajustamos los nombres de las variables para hacerlos más intuitivos y alineados con el propósito de encontrar divisores de un número.
Al final hacemos el análisis temporal y espacial bajo la notación Big O, para poner datos a la eficiencia del resultado.
En el mundo de la informática, entender cómo manipular números y aplicar algoritmos sencillos como este es clave para resolver problemas más complejos.
Feliz programación! ❤️😀
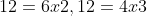
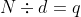
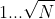
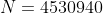
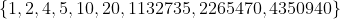
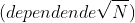
Comments are closed.